Binary Representations
Review of binary representations.
Shortcut for Quick Review:
Update (2020.12.06): Fix typo in answer (Any Number Basis to Decimal)
Number Basis (Radix)
Decimal, Binary, Octal, Hexadecimal are the common number basis seen in Computer Science courses.
- Decimal: All digits are 0 to 9, carry occurs at ten, so each digit has ten different values. (0, 1, …, 9)
- Binary: All digits are 0 to 1, carry occurs at two, so each digit has two different values. (0, 1)
- Octal: All digits are 0 to 7, carry occurs at eight, so each digit has eight different values. (0, 1, …, 7)
- Hexadecimal: All digits are 0 to 15 (F), carry occurs at sixteen, so each digit has sixteen different values. (0, 1, …, 9, A, B, C, D, E, F)
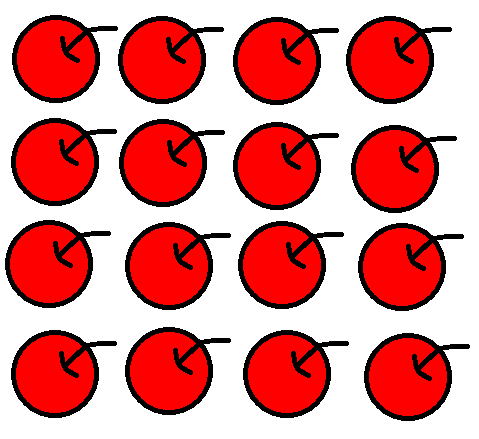
-
So, if we have these apples, counting in Decimal should be:
Click to expand Answer
✔️ Answer

-
Counting in Binary should be:
Click to expand Answer
✔️ Answer

-
Counting in Hexadecimal should be:
Click to expand Answer
✔️ Answer

Integer Conversion between Number Bases
Any Number Basis to Decimal
Since we’re used to Decimal, so converting any other number basis to Decimal is an easy task for us. We can simply multiply each digit by the power of the number basis.
Take sixty one ($61_{10}$, $111101_2$, $\text{3D}_{16}$) as example:
-
Decimal to decimal ($61_{10}$)
Click to expand Answer
✔️ Answer
$10^6$ $10^5$ $10^4$ $10^3$ $10^2$ $10^1$ $10^0$ $0$ $0$ $0$ $0$ $0$ $6$ $1$ In decimal form: $61_{10}=0\cdot 10^2+6\cdot 10^1+1\cdot 10^0=61_{10}$
-
Binary to Decimal ($111101_2$)
Click to expand Answer
✔️ Answer
$2^6$ $2^5$ $2^4$ $2^3$ $2^2$ $2^1$ $2^0$ $0$ $1$ $1$ $1$ $1$ $0$ $1$ In decimal form: $111101_{2}=1\cdot 2^5+1\cdot 2^4+1\cdot 2^3+1\cdot 2^2+0\cdot 2^1+1\cdot 2^0=61_{10}$
-
Hexadecimal to Decimal ($\text{3D}_{16}$)
Click to expand Answer
✔️ Answer
$16^6$ $16^5$ $16^4$ $16^3$ $16^2$ $16^1$ $16^0$ $0$ $0$ $0$ $0$ $0$ $3$ $\text{D}$ In decimal form: $3\text{D}_{16}=0\cdot 16^2+3\cdot 16^1+13\cdot 16^0=61_{10}$
Some more practices:
-
Binary to Decimal ($1010111_2$)
Click to expand Answer
✔️ Answer
$87_{10}$
-
Hexadecimal to Decimal ($\text{6B}_{16}$)
Click to expand Answer
✔️ Answer
$107_{10}$
Decimal to Any Number Basis
Converting to any other number basis is also quite easy. We can simply keep dividing by the number basis and write down the remainder from right to left after each division. This is actually an inverse operation of converting to Decimal.
Take sixty one ($61_{10}$, $111101_2$, $\text{3D}_{16}$) as example:
-
Decimal to Hexadecimal ($61_{10}$)
Click to expand Answer
✔️ Answer
Calculate in Decimal.
$61/16=3….13$, write down $13_{10}$, which is $\text{D}_{16}$.
$16^6$ $16^5$ $16^4$ $16^3$ $16^2$ $16^1$ $16^0$ $\text{D}$ $3/16=0….3$, write down $3_{16}$.
$16^6$ $16^5$ $16^4$ $16^3$ $16^2$ $16^1$ $16^0$ $3$ $\text{D}$ The process is over once the quotient becomes zero.
-
Decimal to Binary ($61_{10}$)
Click to expand Answer
✔️ Answer
Calculate in Decimal.
$61/2=30….1$, write down $1_2$.
$2^6$ $2^5$ $2^4$ $2^3$ $2^2$ $2^1$ $2^0$ $1$ $30/2=15….0$, write down $0_2$.
$2^6$ $2^5$ $2^4$ $2^3$ $2^2$ $2^1$ $2^0$ $0$ $1$ $15/2=7….1$, write down $1_2$.
$2^6$ $2^5$ $2^4$ $2^3$ $2^2$ $2^1$ $2^0$ $1$ $0$ $1$ $7/2=3….1$, write down $1_2$.
$2^6$ $2^5$ $2^4$ $2^3$ $2^2$ $2^1$ $2^0$ $1$ $1$ $0$ $1$ $3/2=1….1$, write down $1_2$.
$2^6$ $2^5$ $2^4$ $2^3$ $2^2$ $2^1$ $2^0$ $1$ $1$ $1$ $0$ $1$ $1/2=0….1$, write down $1_2$.
$2^6$ $2^5$ $2^4$ $2^3$ $2^2$ $2^1$ $2^0$ $1$ $1$ $1$ $1$ $0$ $1$ The process ends since the quotient becomes zero.
Some more practices:
-
Decimal to Binary ($173_{10}$)
Click to expand Answer
✔️ Answer
$10101101_2$
-
Decimal to Hexadecimal ($173_{10}$)
Click to expand Answer
✔️ Answer
$\text{AD}_{16}$
Any Basis to Any Basis
You can use Decimal as an intermediate basis when converting between any two bases. The direct conversion process between any two bases is similar to the process above, but is slightly more difficult. You can try to come up with a direct conversion solution by yourself.
-
Binary to Hexadecimal ($11111011_2$)
Click to expand Answer
✔️ Answer
$\text{FB}_{16}$
-
Hexadecimal to Binary ($\text{AC}_{16}$)
Click to expand Answer
✔️ Answer
$10101100_2$
Binary and Hexadecimal are the number bases commonly used in programming. You can find the special relationship ($2^4=16$) between them, that is each four binary digits can be converted independently into one hexadecimal digit. Base on this observation, you can quickly convert between Binary and Hexadecimal inside you head.
Fraction Conversion between Number Bases
-
Binary to Decimal ($10.1101_2$)
Click to expand Answer
✔️ Answer
$2.8125_{10}$
Follow the same process:
$10.1101_2=6.8125_{10}$
$2^1$ $2^0$ . $2^{-1}$ $2^{-2}$ $2^{-3}$ $2^{-4}$ $1$ $0$ . $1$ $1$ $0$ $1$ In decimal form: $10.1101_2=2+0.5+0.25+0.0625=2.8125_{10}$
-
Decimal to Binary ($3.6875_{10}$)
Click to expand Answer
✔️ Answer
$11.1011_{10}$
This requires some thinking. You can perform the same operation on the digits before the radix point. And then, we clear those converted digits and start multiplying by the basis, while keep taking away the digits before the radix point.
$11.1011_2=3.6875_{10}$
$2^1$ $2^0$ . $2^{-1}$ $2^{-2}$ $2^{-3}$ $2^{-4}$ $1$ $1$ . $1$ $0$ $1$ $1$ In decimal form:
$0.6875\cdot 2=1+0.375$
$0.375\cdot 2=0+0.75$
$0.75\cdot 2=1+0.5$
$0.5\cdot 2=1+0.0$
-
Decimal to Binary ($0.87_{10}$)
Click to expand Answer
✔️ Answer
$0.11011110….$
Some numbers cannot be represented precisely using other number bases. This also happens in some Decimal fractions.
Online calculators can be found here:
Binary Representations
Representation of Integers
Now we know how to represent positive integers in binary format, but how about negative integers?
We can simply add a bit to represent whether the number is negative. However, it’s not straight forward to do additions and subtractions at the hardware level.
So we use 2’s complement representation to make addition easier. The concept is simple, we want $N + (-N) = 0$, so if we have the binary representation of $N$, we can calculate $(-N)$ by inverting the digits and adding one.
-
What is the 2’s complement binary representation of $(-6)_{10}$ if we have a total of four bits?
Click to expand Answer
✔️ Answer
$1010_2$
So if we add $6_{10}$ with $(-6)_{10}$,
0110 +1010 ------ 0000The carry bit is discarded.
4-bit 2’s Complement Table:
| Bit Pattern | 2’s Complement |
|---|---|
| 0111 | 7 |
| 0110 | 6 |
| … | … |
| 0010 | 2 |
| 0001 | 1 |
| 0000 | 0 |
| 1111 | -1 |
| 1110 | -2 |
| … | … |
| 1001 | -7 |
| 1000 | -8 |
It’s easy to observe that the representable range for $N$-bit signed integer is $[-2^{N-1}, 2^{N-1}-1]$. The fact that the positive range is smaller than the negative range can be easily seen by the left-most bit since the number $0$ is only represented once, leaving an additional entry for storing $-2^{N-1}$.
Representation of Fractions
For representing fractions, we can simply use a signed-bit since the addition cannot be simplified as seen in 2’s complement.
Floating-point representation is used instead of Fixed-point representation to increase the representable range.
We can further use Excess Notation to speed up the comparison between numbers. The concept is to make the exponent term directly comparable through bit-patterns, that is, make the bit pattern of the smallest representable exponent as $0…0$, and keep adding up. This exponent is put in front of the mantissa so that we can compare two floating-points like integers. See the table below:
Excess-8 Notation Table:
| Bit Pattern | Excess-8 Notation |
|---|---|
| 1111 | 7 |
| 1110 | 6 |
| … | … |
| 1010 | 2 |
| 1001 | 1 |
| 1000 | 0 |
| 0111 | -1 |
| 0110 | -2 |
| … | … |
| 0001 | -7 |
| 0000 | -8 |
-
What is the floating-point representation of $-2.625_{10}$, with 4-bit fraction and 3-bit exponent using the IEEE Standard.
Click to expand Answer
✔️ Answer
$11010101_2$
$-2.625_{10}=-10.101_2=-1.0101_2 \cdot (2_{10})^{1_2}$
Sign Exponent Fraction (Mantissa) 1 101 0101 The
Sign,Exponent,Mantissaorder here makes the number comparable as if they were 2’s complement integers. -
What is the truncation error of $0.1_{10}$ (direct truncation), with 4-bit fraction and 3-bit exponent using the IEEE Standard?
Click to expand Answer
✔️ Answer
$0.00234375$
$0.1_{10}=0.000110011…_2=1.10011…_2\cdot(2_{10})^{-4_2}$
Sign Exponent Fraction (Mantissa) 0 000 1001 Converting back: $1.1001_2\cdot (2_{10})^{-4_2}=0.09765625$ $|0.1-0.09765625|=0.00234375$
The direct truncation is used for simplicity, different rounding techniques are used in the real world.
For further information, there’s also a method for 2’s complement multiplication, which is much harder to think intuitively. And there’s also a 1’s complement representation, which is quite straight forward. For floating-point, there are additional representations such as: Infinities, NaNs and Denormalized Numbers.
To wrap up, the commonly used representations are:
- Signed Magnitude
- One’s Complement
- Two’s Complement
- Excess-N Notation
Overflow & Underflow & Truncation
-
In unsigned representation
When two unsigned numbers are added, overflow occurs if there is a carry out of the leftmost bit.
-
In signed 2’s complement representation
Overflow occurs when both operands are positive and the result is negative. Or both operands are negative but the result is positive.
-
In float representation
Underflow occurs when the result of a floating-point representation is smaller than the smallest value representable.
When a number cannot be precisely represented, the number is truncated.
Try it by Yourself
Here’s a C code that shows the binary representation of any variable.
#include <stdio.h>
#include <limits.h>
void printBits_LittleEndian(size_t const size, void const* const ptr) {
unsigned char* b = (unsigned char*) ptr;
unsigned char byte;
int i, j;
for (i = size - 1; i >= 0; i--) {
for (j = 7; j >= 0; j--) {
byte = (b[i] >> j) & 1;
printf("%u", byte);
}
}
puts("");
}
void printBits_BigEndian(size_t const size, void const* const ptr) {
unsigned char* b = (unsigned char*) ptr;
unsigned char byte;
int i, j;
for (i = size - 1; i >= 0; i--) {
for (j = 0; j < 8; j++) {
byte = (b[i] >> j) & 1;
printf("%u", byte);
}
}
puts("");
}
int main(void) {
int i = 23;
unsigned int ui = UINT_MAX;
float f = 23.45f;
puts("For Little-Endian:");
printBits_LittleEndian(sizeof i, &i);
printBits_LittleEndian(sizeof ui, &ui);
printBits_LittleEndian(sizeof f, &f);
// puts("For Big-Endian:");
// printBits_BigEndian(sizeof i, &i);
// printBits_BigEndian(sizeof ui, &ui);
// printBits_BigEndian(sizeof f, &f);
return 0;
}
The output should be:
For Little-Endian:
00000000000000000000000000010111
11111111111111111111111111111111
01000001101110111001100110011010
If your output is different from above, try un-commenting the Big Endian code below and see the results. This part is just for fun and you can see the actual binary representation for any type of variable. You’ll learn more about Endians in Computer Architecture course.
If you look closely enough, you’ll find that IEEE-754 actually uses an Excess-127 (127 bias) notation instead of Excess-128. If you are interested in the rationale of this, see:
By thinking the process inside out and think of the intuition behind the representations, you never need to memorize these representations or calculations.
For the next assignment, we’ll review the basic concept of arrays and pointers.
Epilogue
Q: Why do programmers confuse Halloween and Christmas?
A: Because Oct 31 equals Dec 25.
Comments