Basic Recursions with C

Review of basic recursions. This part is more conceptual than the previous sections.

Shortcut for Quick Review:

• Toggle all answers (Click to expand/collapse all Answers)

Update (2020.12.05): Fix stack size in answer code (Replace Recursion with Loops)

Steps for Writing Recursion Code

Recursion in programming is like induction in mathematics. So, if you have trouble understanding recursion, maybe you can start by reviewing the concept of mathematical induction.

Every good recursion code writing consists of four parts or steps. The first step is called “The Goal”. The programmer defines a function prototype that can solve the problem once implemented correctly. But of course… the function isn’t implemented yet. The second step is called “The Basic Case”. The programmer solves the simplest case to ensure the termination of recursion calls in later steps. The third step is called “The Inductive Case”. The programmer solves other complicated cases by breaking it down to simpler cases that utilize the defined function as if it is already fully implemented. This takes the ordinary basic case and uses it to do something extraordinary. The code works now, but, the programmer doesn’t have an intuition on why it works yet. He or she should think over the code and convince himself or herself why the code works. That’s why every recursion code writing should have the fourth step, the most important but so easily forgotten part, the part we call “The Intuition”.

– Imitation Quote Christopher Priest in The Prestige

Steps	Recursion	Induction
The Goal	What does the function do	$f(n)$ have some certain properties
The Basic Case	if (n == 1) return ...;	prove $f(1)$ satisfies the properties
The Inductive Case	else func(n-1); return ...;	prove $f(n)$ satisfies the properties, by assuming $f(k)$ works $\forall k \in [1,n-1]$
The Intuition	Rethink the intuition	on why it works

Let’s take the classic Tower of Hanoi as an example.

Tower of Hanoi

The objective of the puzzle is to move the entire stack from rod-1 to rod-3, obeying the following simple rules:

• Only one disk can be moved at a time.
• Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
• No larger disk may be placed on top of a smaller disk.

Now, we want to output the solution in text format, let’s follow the 4 steps.

1. “The Goal”: Define a function prototype that can solve the problem once implemented correctly.

   Define the function prototype and what does it do.

   Click to expand Answer

   ✔️ Answer

   void move_hanoi(int n, int from, int to, int temp);
   

   This function moves $n$ disks on the top of the from rod to the to rod legally. (without violating the rules) The temp rod only has disks that are larger than the top $n$ disks, so it can be used to temporarily store disks as if the rod is empty. We assume this function is implemented correctly. So if the problem is to move 3 disks from rod-1 to rod-3, we can achieve it by a single function call, move_hanoi(3, 1, 3, 2)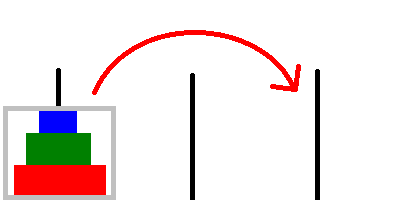

   

   

   This part should be the hardest part since the function definition may be tricky to define. Sometimes we even need to think about how to deal with the induction / recursive case and then we can think of this function definition.

2. “The Basic Case”: Solve the simplest case to ensure the termination of recursion calls in later steps.

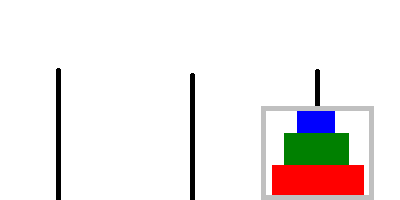
   Assume that we are only required to move a single disk, how should we move it.

   Click to expand Answer

   ✔️ Answer

   // Move the disk directly to the target rod.
   printf("Move disk %d from %d to %d\n", 1, from, to);
   

   If we have only one disk, any move is legal.

   

   

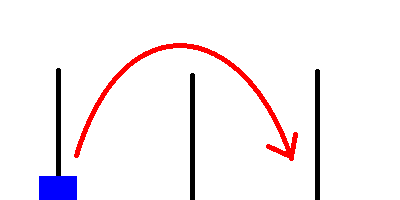
   Once this basic case is implemented, we can use it without worrying about infinite recursion.

3. “The Inductive Case”: Solve other complicated cases by breaking it down to simpler cases that utilize the defined function as if it is already fully implemented.

   Since the basic case is implemented, we now assume that move_hanoi(1, ...), move_hanoi(2, ...), move_hanoi(n-1, ...) are all implemented. Now we can use them to move the $n$ disks. It’s similar to strong mathematical induction here.

   Keep in mind that we can use move_hanoi for $[1,n-1]$ as if it’s already implemented. You can use it freely like printf or strlen, without worrying that the function isn’t fully implemented yet.

   The importance of this thought is ofter underrated. Some students may think: “I haven’t implemented this function yet, why can I call it?”, then they start writing codes that can be done by a simple recursion function call. By doing so, they’ll eventually find out that they need to write infinite lines of code if they do not utilize the recursion function call.

   If you know mathematical induction, you can write the code like writing mathematical proofs. As long as the recursion function calls only use $f(k)$, $\forall k\in [1,n-1]$, the call will be correct.

   Recall the definition of the function.

   void move_hanoi(int n, int from, int to, int temp);
   

   This function moves $n$ disks on the top of the from rod to the to rod legally. (without violating the rules) The temp rod only has disks that are larger than the top $n$ disks, so it can be used to temporarily store disks as if the rod is empty.

   And now, for the inductive/recursive case:

   Click to expand Answer

   ✔️ Answer

   // Keep the largest disk below and move the upper disks to the temporary rod.
   move_hanoi(n - 1, from, temp, to);
   // Move the largest disk to the target destination.
   printf("Move disk %d from %d to %d\n", n, from, to);
   // Stack the upper disks above the largest disk.
   move_hanoi(n - 1, temp, to, from);
   

   The temp rod may not be empty, but we can still temporarily store disks on it since the disks on it are larger than the disks that we’re currently moving.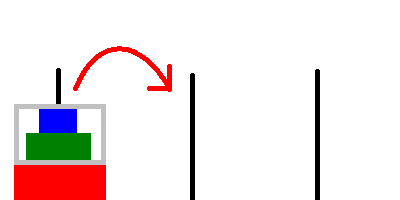

   

   

   

   

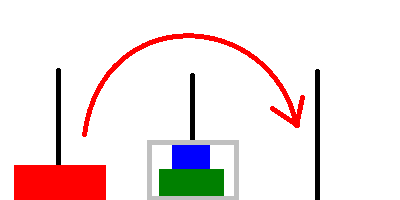
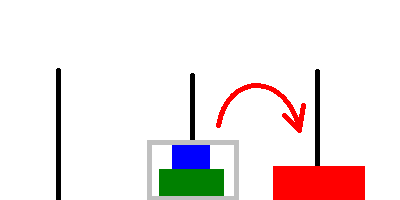
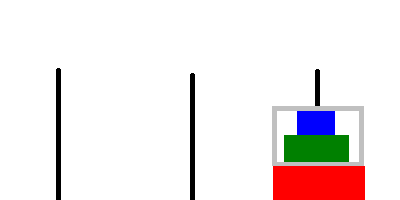
4. “The Intuition”: The code works now, but, the programmer doesn’t understand why it actually works yet. He or she should think over the code and convince himself or herself why the code works.

   Explain the entire code to yourself and convince yourself of its correctness.

   Click to expand Answer

   ✔️ Answer

   // This function moves $n$ disks on the top of the `from` rod to the `to` rod legally. (without violating the rules) The `temp` rod only has disks that are larger than the top $n$ disks, so it can be used to temporarily store disks as if the rod is empty.
   void move_hanoi(int n, int from, int to, int temp);
   void move_hanoi(int n, int from, int to, int temp) {
       if (n == 1)
           // If there are only one disk to move,
           // Move the disk directly to the target rod.
           printf("Move disk %d from %d to %d\n", 1, from, to);
       else {
           // If there are multiple disks to move,
           // Keep the largest disk below and move the upper disks to the temporary rod.
           move_hanoi(n - 1, from, temp, to);
           // Move the largest disk to the target destination.
           printf("Move disk %d from %d to %d\n", n, from, to);
           // Stack the upper disks above the largest disk.
           move_hanoi(n - 1, temp, to, from);
       }
   }
   

   Think over the entire process and find out that the code we write is equivalent to proving the correctness through mathematical induction.

5. Bonus Section: Time Complexity Analysis

   Analyze how many movements occur.

   Click to expand Answer

   ✔️ Answer

   Assume we have $n$ disks, and each move requires $c$ time.

   \[\begin{align} T(0) &= 0 \\\\ T(1) &= c \\\\ T(n) &= 2\cdot T(n-1)+c \\\\ &= 2\cdot 2\cdot T(n-2)+2\cdot c+c \\\\ &= 2\cdot 2\cdot 2\cdot T(n-3)+4\cdot c+2\cdot c+c \\\\ &= 2^n \cdot T(0) + \sum_{k=0}^{n-1}(2^k\cdot c) \\\\ &= c\cdot \sum^{n-1}_{k=0}2^k \end{align}\]

   Sum of geometric sequence:

   \[\sum^{n-1}_{k=0}2^k=\frac{2^0 \cdot (1-2^{n-1})}{1-2}=2^n-1\] \[T(n)=(2^n-1)\cdot c\]

   We proved that the time complexity is $O(2^n)$, total $2^n-1$ moves. This part is a bonus section, you’ll learn more about it in the Design and Analysis of Algorithm course.

Here’s a nice image from Wikipedia.

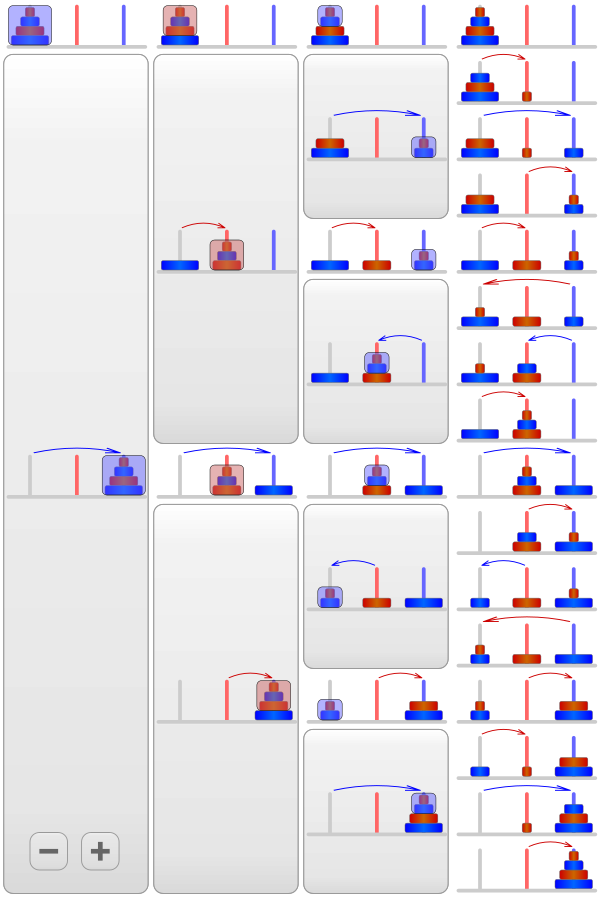
The leftmost column is “The Goal”. It defines the function and uses it as a black box, we only need to know what it does, without knowing how it does it.

The second column (counting from left) is “The Recursion Case”. It uses the function as if it is implemented, but only use $f(k)$, $\forall k\in [1,n-1]$. (Does not use $f(n)$)

The bottom-right part is “The Basic Case”, we can just move the disk directly.

For other parts, it enumerates each move. It is almost impossible to enumerate this in our head for a large enough $n$. So we can use recursion to abstract this part and prove its correctness.

There are many other solutions that can solve the Tower of Hanoi problem, feel free to come up with other solutions on your own. The solution shown here is the simplest and straightforward one in my opinion.

Variable Scopes and Function Call Stack

Note that all variables in each recursive function call are a new local variable with its own scope.

For the first move in a $n=3$ Tower of Hanoi problem, we can visualize the call stack of the first call to basic case as below.

move_hanoi(3, 1, 3, 2);

void move_hanoi_depth1(int n1=3, int from1=1, int to1=3, int temp1=2) {
    move_hanoi_depth(n1 - 1, from1, temp1, to1);
    // The call above is shown as 'move_hanoi_depth2` below.
    printf("Move disk %d from %d to %d\n", n1, from1, to1);
    move_hanoi_depth(n1 - 1, temp1, to1, from1);
}
void move_hanoi_depth2(int n2=2, int from2=1, int to2=2, int temp2=3) {
    move_hanoi_depth(n2 - 1, from2, temp2, to2);
    // The call above is shown as 'move_hanoi_depth3` below.
    printf("Move disk %d from %d to %d\n", n2, from2, to2);
    move_hanoi_depth(n2 - 1, temp2, to2, from2);
}
void move_hanoi_depth3(int n3=1, int from3=1, int to3=3, int temp3=2) {
    printf("Move disk %d from %d to %d\n", 1, from3, to3);
    // This function will return to 'move_hanoi_depth2' above, and continue running the subsequent codes.
}

The bottom graph is the full call/return order of the case with 3 disks.

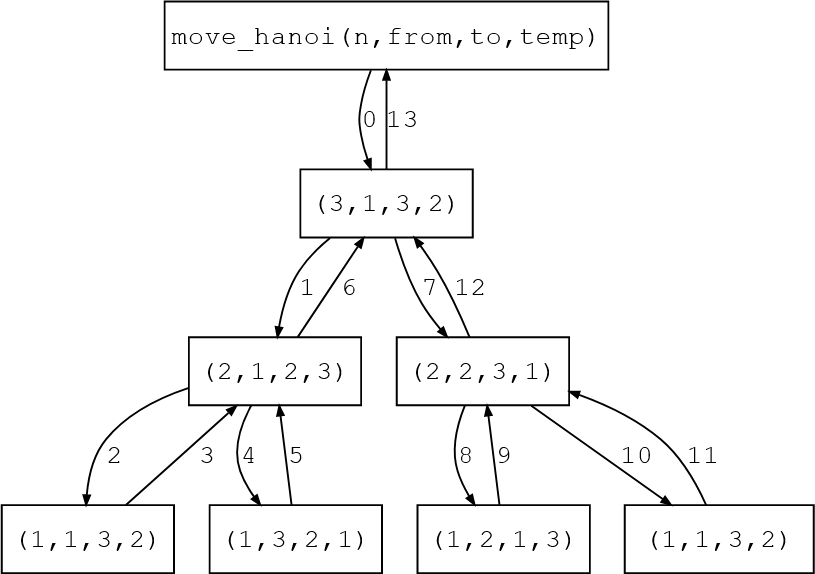
You may observe that the $n=1$, $n=2$, $n=3$ vertices in the graph above corresponds to the movements of the green, blue, red disk in the figure below, respectively.

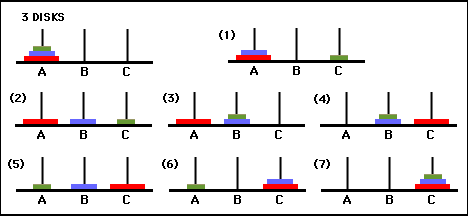
Photo Credit: Tower of Hanoi on The Math Forum

With the knowledge of variable scopes, function stacks and mathematical induction, you should have the ability to write recursion codes for most problems.

Replace Loops with Recursion

for loops and recursion is interchangeable. However, recursion has higher overhead due to many function calls, you’ll learn more about it in the Computer Architecture course.

The following code is the code of Selection Sort using for loop.

#include <stdio.h>
#define MAX 10
#define swap(a, b) if (a != b) {(*a)^=(*b); (*b)^=(*a); (*a)^=(*b);}

void selection_sort(int* a, int size);
int a[MAX] = {3, 7, 9, 1, 4, 0, 8, 6, 2, 5};

int main(void) {
    selection_sort(a, MAX);
    for (int i = 0; i < MAX; i++) {
        printf("%d ", a[i]);
    }
    return 0;
}

void selection_sort(int* a, int size) {
    int i, j, min_idx;
    // Put the i-th smallest number in a[i].
    for (i = 0; i < size - 1; i++) {
        // Scan through the remaining array and pick the smallest element.
        min_idx = i;
        for (j = i+1; j < size; j++) {
            if (a[min_idx] > a[j])
                min_idx = j;
        }
        // Swap the smallest number to the left.
        swap(&a[i], &a[min_idx]);
    }
}

Modify the code to use recursion without using any explicit loops (while, for).

Click to expand Answer

✔️ Answer

First, remove the outer loop.

#include <stdio.h>
#define MAX 10
#define swap(a, b) if (a != b) {(*a)^=(*b); (*b)^=(*a); (*a)^=(*b);}

void selection_sort(int* a, int size);
int a[MAX] = {3, 7, 9, 1, 4, 0, 8, 6, 2, 5};

int main(void) {
    selection_sort(a, MAX);
    for (int i = 0; i < MAX; i++) {
        printf("%d ", a[i]);
    }
    return 0;
}

void selection_sort(int* a, int size) {
    int j, min_idx;
    if (size == 1)
        // No need to sort a single number.
        return;
    // Scan through the remaining array and pick the smallest element.
    min_idx = 0;
    for (j = 1; j < size; j++) {
        if (a[min_idx] > a[j])
            min_idx = j;
    }
    // Swap the smallest number to the first.
    swap(&a[0], &a[min_idx]);
    // Since the first element is smallest, we can sort the remaining array recursively.
    selection_sort(a+1, size-1);
}

Second, remove the inner loop.

#include <stdio.h>
#define MAX 10
#define swap(a, b) if (a != b) {(*a)^=(*b); (*b)^=(*a); (*a)^=(*b);}

int get_min_idx(int* a, int size);
void selection_sort(int* a, int size);
int a[MAX] = {3, 7, 9, 1, 4, 0, 8, 6, 2, 5};

int main(void) {
    selection_sort(a, MAX);
    for (int i = 0; i < MAX; i++) {
        printf("%d ", a[i]);
    }
    return 0;
}

int get_min_idx(int* a, int size) {
    if (size == 1)
        return 0;
    int min_idx = get_min_idx(a+1, size-1) + 1;
    if (a[min_idx] > a[0])
        return 0;
    return min_idx;
}

void selection_sort(int* a, int size) {
    int min_idx;
    if (size == 1)
        // No need to sort a single number.
        return;
    // Get the smallest element.
    min_idx = get_min_idx(a, size);
    // Swap the smallest number to the first.
    swap(&a[0], &a[min_idx]);
    // Since the first element is smallest, we can sort the remaining array recursively.
    selection_sort(a+1, size-1);
}

Replace Recursion with Loops

The following code is the Tower of Hanoi code using recursion.

#include <stdio.h>

void move_hanoi(int n, int from, int to, int temp);

int main(void) {
    move_hanoi(3, 1, 3, 2);
    return 0;
}

void move_hanoi(int n, int from, int to, int temp) {
    if (n == 1)
        // If there are only one disk to move,
        // Move the disk directly to the target rod.
        printf("Move disk %d from %d to %d\n", 1, from, to);
    else {
        // If there are multiple disks to move,
        // Keep the largest disk below and move the upper disks to the temporary rod.
        move_hanoi(n - 1, from, temp, to);
        // Move the largest disk to the target destination.
        printf("Move disk %d from %d to %d\n", n, from, to);
        // Stack the upper disks above the largest disk.
        move_hanoi(n - 1, temp, to, from);
    }
}

Modify the code to use loops without recursions.

Click to expand Answer

✔️ Answer

#include <stdio.h>
#define MAX 10000

typedef struct {
    int n, from, to, temp;
} Record;
Record stack[MAX];
int top = -1;

void move_hanoi(int n, int from, int to, int temp);

int main(void) {
    move_hanoi(3, 1, 3, 2);
    return 0;
}

void move_hanoi(int n, int from, int to, int temp) {
    stack[++top] = (Record) {n, from, to, temp};
    while (top != -1) {
        Record record = stack[top--];
        if (record.n == 1 || record.temp == -1) {
            printf("Move disk %d from %d to %d\n", record.n, record.from, record.to);
            continue;
        }
        stack[++top] = (Record) {record.n - 1, record.temp, record.to, record.from};
        stack[++top] = (Record) {record.n, record.from, record.to, -1};
        stack[++top] = (Record) {record.n - 1, record.from, record.temp, record.to};
    }
}

Local vs. Global Variables in Recursion

For recursion functions, it’s better to only use local variables to avoid misconceptions. Only using local variables can keep your code clean and keep the structure of mathematical induction.

However, accessing global variables may make your code simpler in some cases, but use it in caution.

For the next assignment, we’ll review binary representations.

Epilogue

You can try to learn and implement N-Queens, Binary Search, Merge Sort, Quick Sort, etc by yourself, following the 4 main steps mentioned above. The concept of recursion not only needs a lot of practice but also requires some critical thinking. After your code got AC, it’s better to think your code all over again and review how it works exactly.

Photo Credit: Screenshot of Google Search page.